
因式分解到底有多重要!
因式分解是代数的重要知识点,与代数式、方程、函数都有密切的联系。因式分解本质上是整式乘法的逆运算,并且分解的技巧非常丰富,是初中数学的重点和难点知识!
重点和难点?很多孩子并不会认同!因为初中数学对因式分解,只要求学生掌握提取公因式和两个乘法公式而已!
但是,对于以代数为主的高中的数学而言,因式分解包含了丰富的代数处理技巧,是及其重要和基础的知识!
另外,比较尴尬的是,只有少部分优质高中会在高一开学初设置初高中衔接课程,来补习因式分解的技巧。绝大部分高中会默认学生在初中学习已经过因式分解了!
至此,当高中老师用娴熟的代数技巧处理代数问题时,很多孩子就开始懵了,孩子们的高中数学就是在这种感觉中逐渐跟不上节奏的!

因式分解技巧大全
代数中只有两个问题:消元与降次!因式分解最大的意义就是降次!
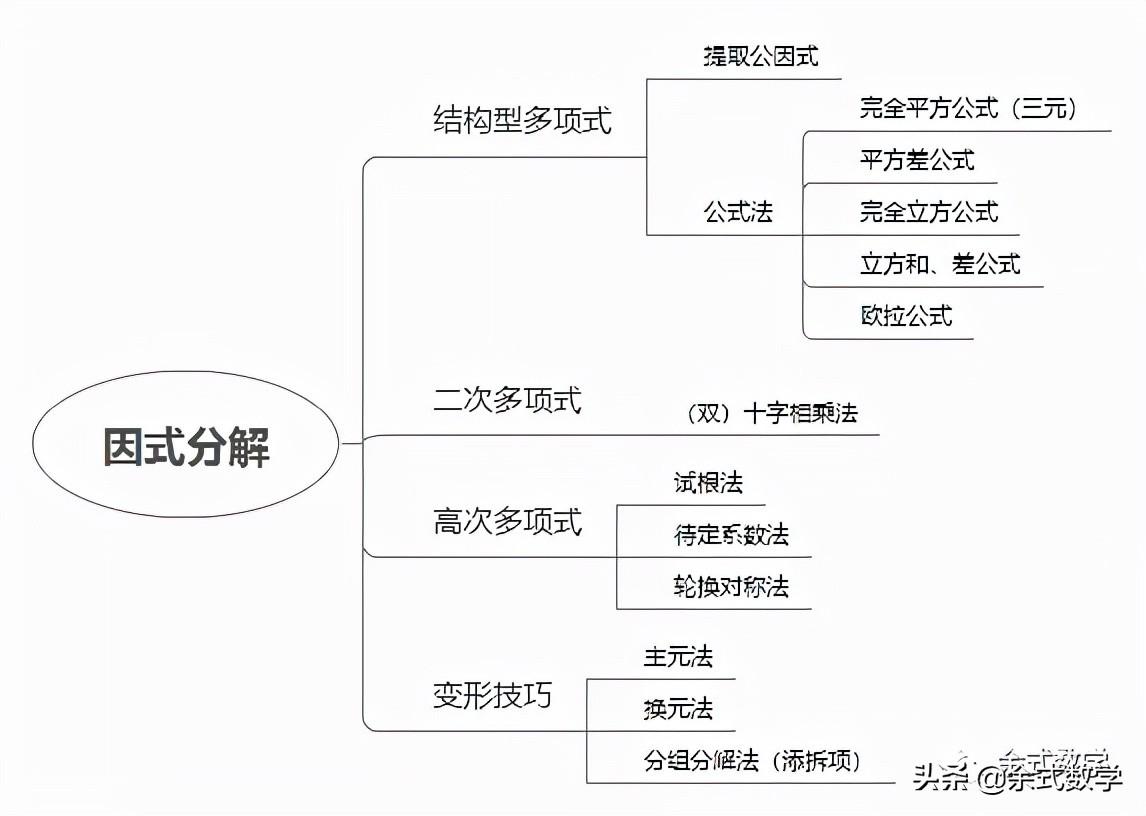
对于分解的因式,大体上可以分为三类:结构型多项式、二次多项式、高次多项式!
①什么是结构型多项式?这里指的是能够提取公因式和利用整式乘法公式的结构。对于这种结构型多项式,只需要利用“提取公因式”和“公式法”即可处理。
②二次多项式包含什么呢?这里的二次多项式指的是多项式中某一个字母的最高次数为二的多项式,这类问题都可以利用“十字相乘法”进行处理!
在这类多形式中,是一元还是多元一直都不重要,因为在“主元法”的方法论中,所有代数式中只有一个字母!
③高次多项式指的是多项式的次数高于二次的的多项式,主要是三次多项式和四次多项式。
这类多项式的分解主要是利用因式定理的“试根法”来处理。对于四次及以上次数,在“试根法”无法分解时,可以假设特定结构,使用“待定系数法”来分解多项式。
除此之外,还有一些常用的分解技巧,例如前面提到的主元法、换元法、分组分解法(添拆项),这些方法不能直接因式分解,但是能将多项式进行简化到可以使用其它方法分解。
完结《李铁柱苏清月》醉在风花雪月小说全章节目录阅读 (醉在风花雪月)小说全集免费在线阅读

创维(SKYWORTH)冰箱售后服务热线及保养指南(创维(SKYWORTH)冰箱冰箱门一关上就轰隆隆的响)

brandt冰箱维修热线24小时咨询服务热线(brandt冰箱冰箱不制冷的原因及解决办法)

冰松洗衣机全国24小时售后维修服务客服热线(冰松洗衣机洗衣机脱水转速慢是咋回事)

楚雨薇小说_(文科学长)完整版阅读 小说全集免费在线阅读(文科学长)

普雪热水器400服务号码全国售后的热线实时反馈-今-日-汇-总(普雪热水器热水器最新价格表)

多特智能锁全国(24小时)各售后受理客服中心(多特智能锁确认开锁方式)

完结文躺平的我被祖龙偷听心声最新章节列表_完结文躺平的我被祖龙偷听心声全文免费阅读(夏无且嬴政)
