
向量的知识
向量定义: 向量是一条有方向的线段(有长度和确定方向的线段)。 图形化的向量,表示成一定长度的有向线段。
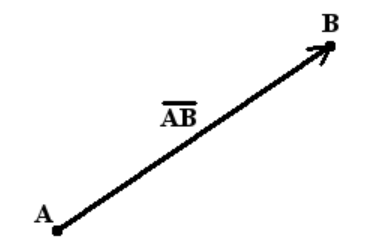
具有起始点A和结束点B的向量,记为AB。向量也可以用一个小写字母,例如a表示。
向量的长度: 有向线段的长度决定了向量的数值,称为向量AB的长度。
向量AB的长度记为:|AB|。
共线向量: 平行于一条直线或落在一条直线上的向量称为共线向量
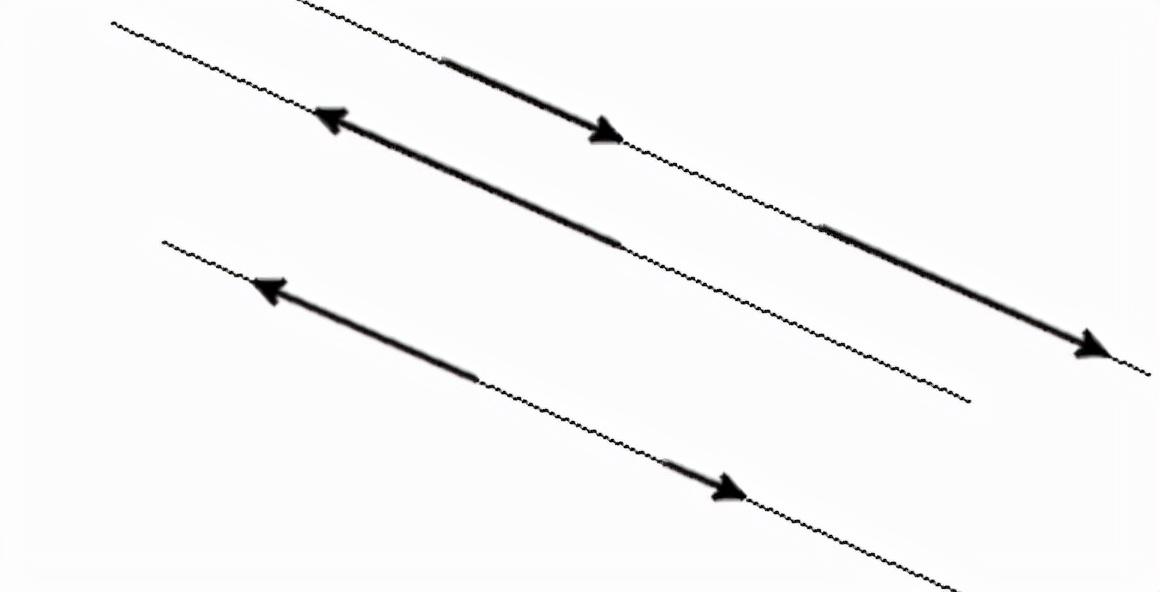
共面向量:平行于同一平面的向量,或位于同一平面上的向量称为共面向量。
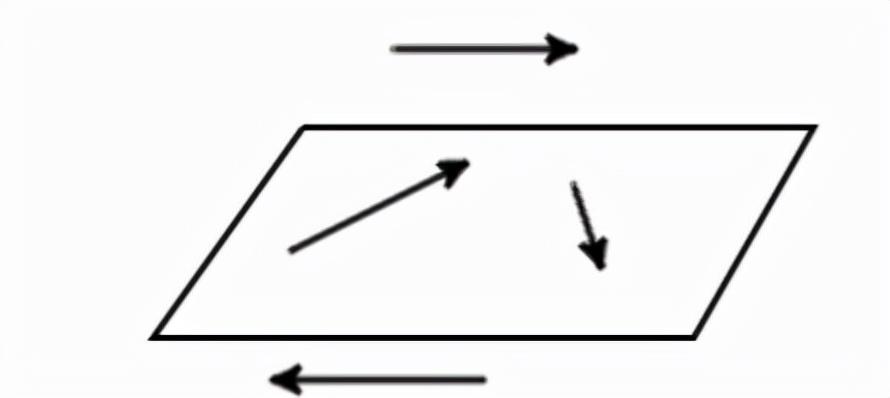
向量相等: 向量a和b是相等的如果它们在同一条或平行线上,它们的方向相同长度相等。
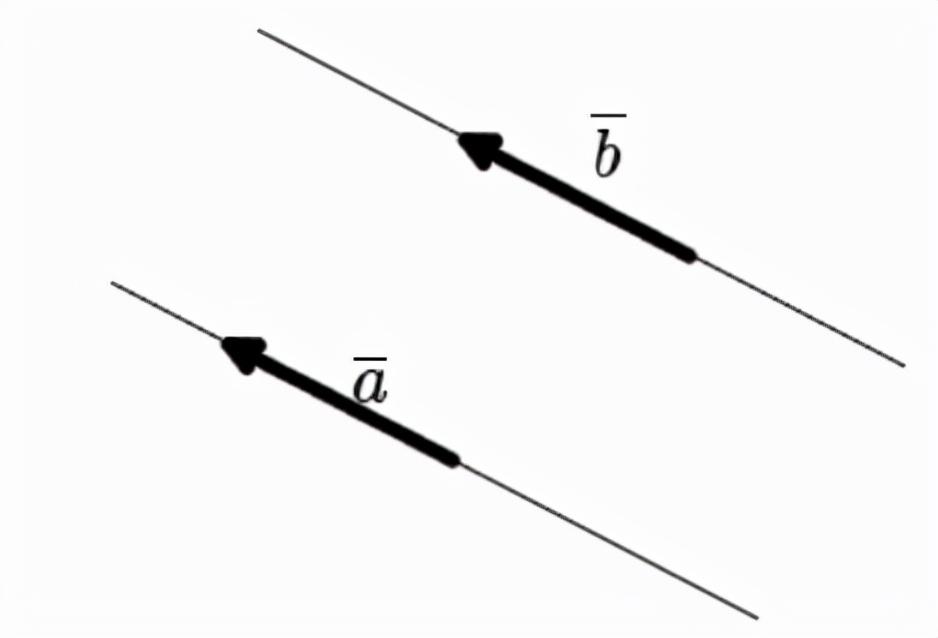
单位向量: 单位向量或向量角是长度等于1的向量。
平面问题的向量坐标公式
在平面问题中,向量AB由点A(Ax; Ay) 和B(Bx; By) 可以用下面的公式确定:
AB = {Bx - Ax ; By - Ay}
空间问题的向量坐标公式
在空间问题中,向量AB由点A(Ax; Ay; Az)和B(Bx; By; Bz)可以用下列公式确定:
AB = {Bx - Ax ; By - Ay ; Bz - Az}
二维向量的向量长度公式
在平面问题中,向量a的长度= {ax; ay}可以用下面的公式计算:
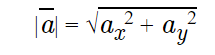
三维向量的向量长度公式
在空间问题中,向量a的长度= {ax; ay; az}可用以下公式计算:
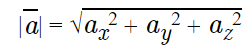
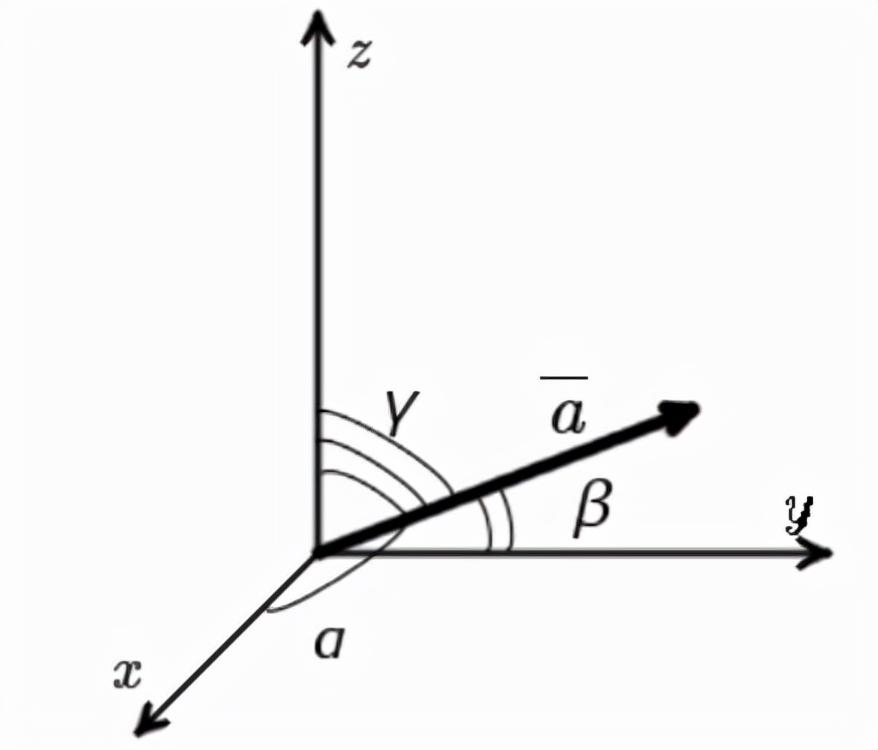
二维矢量的方向余弦公式
在平面问题中,向量a的方向余弦= {ax; ay}可以用下面的公式确定:
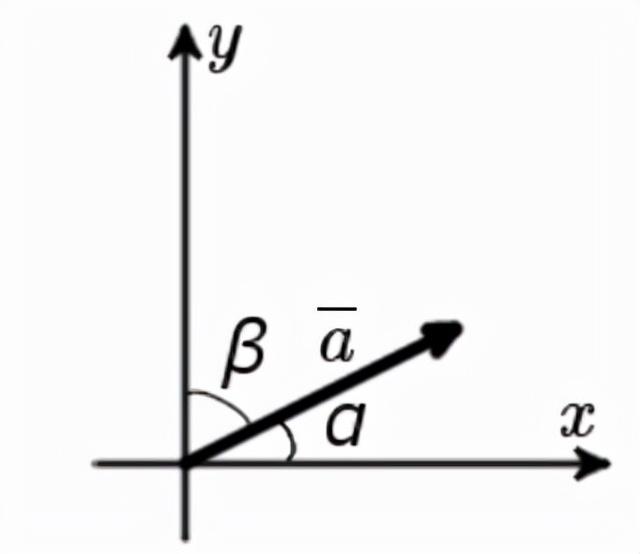
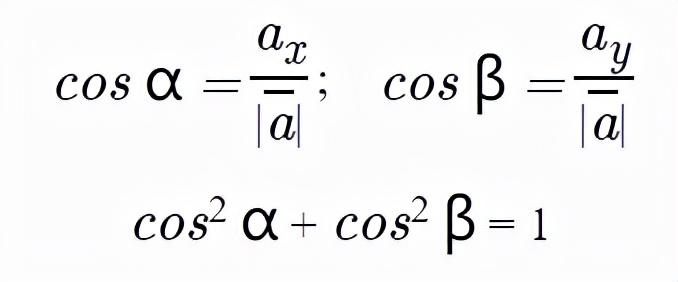
在空间问题中,向量a的方向余弦= {ax ; ay ; az}可以用下面的公式确定:

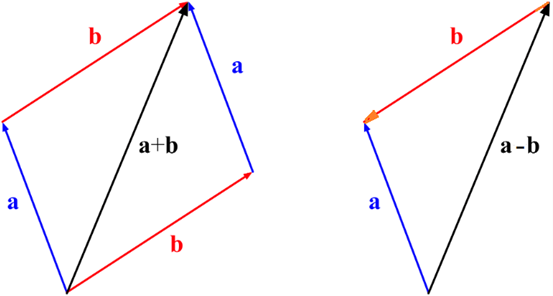
平面问题的向量加减公式
在平面问题中,向量a = {ax; ay}和b = {bx; by}的和或差可 通过下面的公式确定:
在空间问题中,向量a ={ax ; ay ; az}和b = {bx ; by ; bz}的和或差可通过下面的公式确定:
a + b = {ax + bx; ay + by; az + bz}
a - b = {ax - bx; ay - by; az - bz}
向量a和b的点积几何解释: 两个向量a和b的点积是一个标量,等于向量的大小之积乘以向量夹角的余弦值。
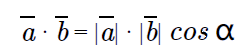
平面问题的点积公式
在平面问题中向量a = {ax; ay }和b = {bx; by}通过下面的公式确定:
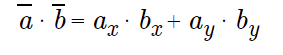
空间问题的点积公式
在空间问题中向量a = {ax ; ay ; az}和b ={bx ; by ; bz}通过下面的公式确定:
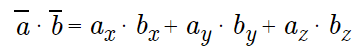
霍克利夫人 新书《叶姝谢泽》小说全集阅读

[误圆房后,冷面军官宠她入骨]林夏陆北霆小说全文章节目录在线阅读

bosch空调24小时全国售后热线实时反馈-今-日-更-新(bosch空调空调e享模式 )

雪菲特空调售后服务热线(各区/24小时)统一客服热线(雪菲特空调空调遥控器显示 )

KELON空调售后服务维修号码实时反馈-今-日-更-新(KELON空调空调显示EH故障码,怎么处理? )

惠康中央空调全市维修热线号码24h服务(惠康中央空调模块保护 )

松下空调全国统一服务号码-全国服务热线实时反馈-今-日-更-新(松下空调室内外电控(新老平台)通讯协议不匹配 )

七星空调24小时全国售后热线实时反馈全+境+到+达(七星空调排气温度过高 )
